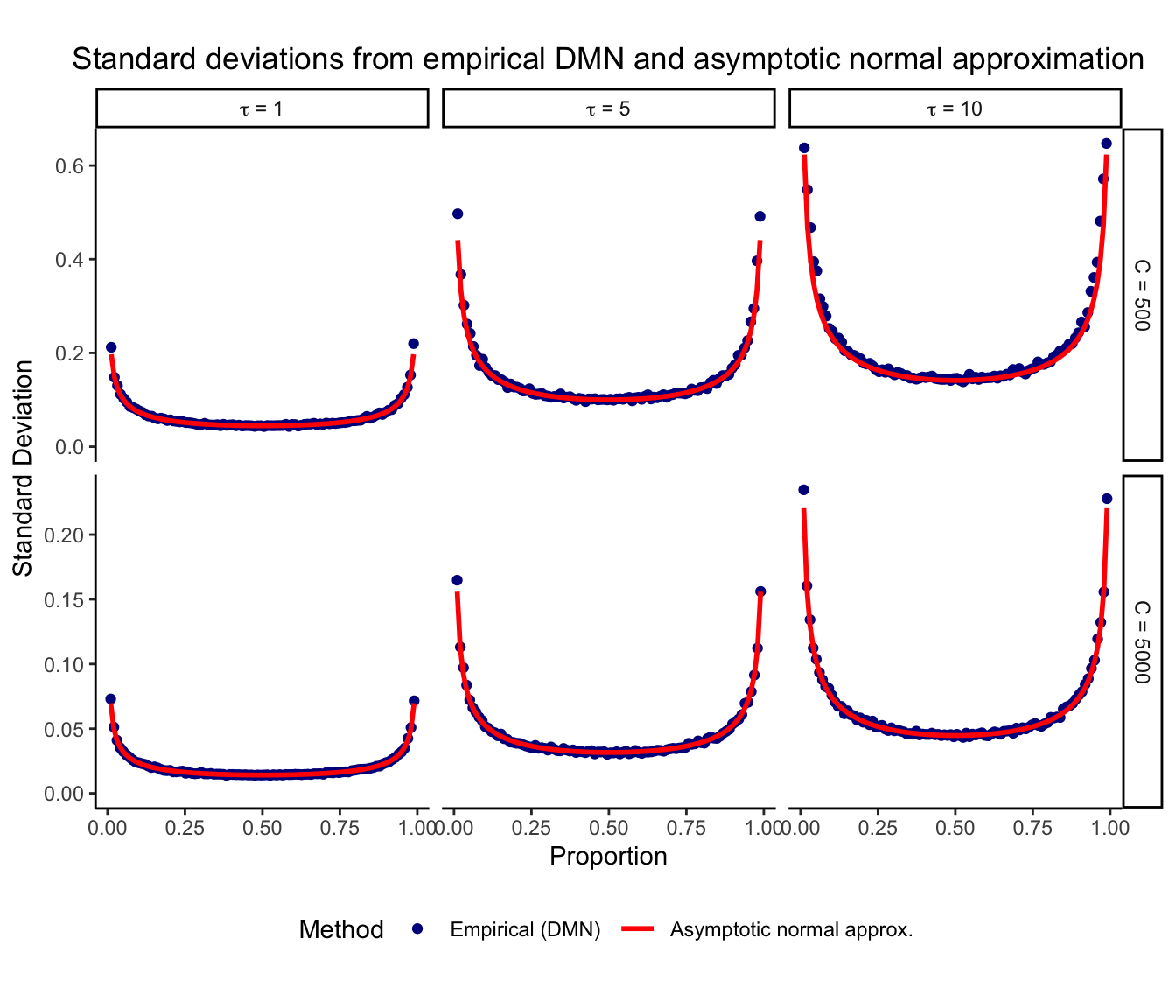
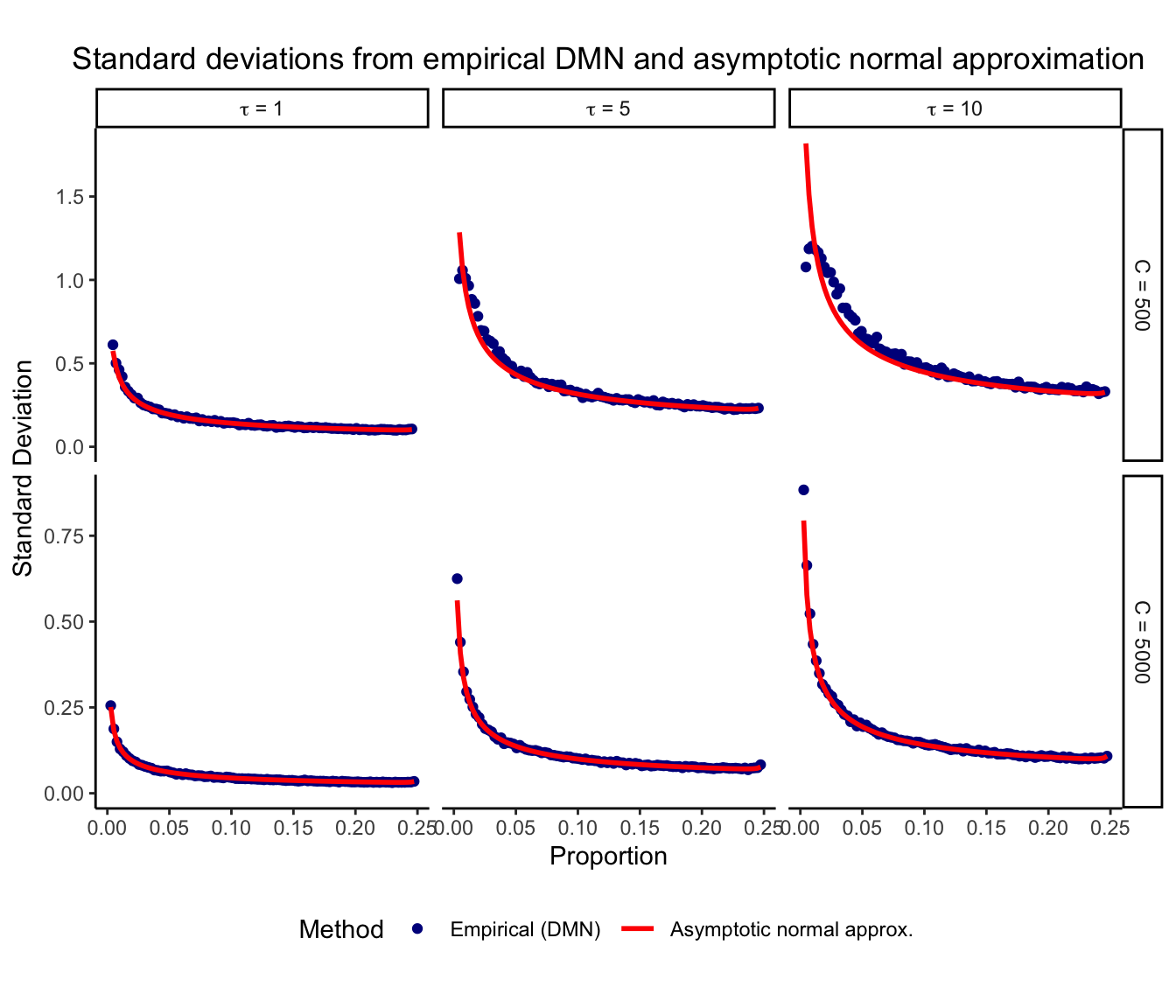
Normal approximation vs. empirical simulation
Developed by Gabriel Hoffman
Run on 2025-02-17 21:01:24.858131
Source:vignettes/crumblr_theory.Rmd
crumblr_theory.RmdAsymptotic normal approximation
Let the vector ${\bf p}$ be the true fractions across categories. Consider total counts sampled from a Dirichlet-multinomial (DMN) distribution with overdispersion , where reduces to the multinomial distribution. The centered log ratio (CLR) of the estimated fraction in ${\bf \hat p}$ is
$$\begin{equation} \tag{1} \text{clr}_i({\bf \hat p}) = \log(\hat p_i) - \frac{1}{D}\sum_{j=1}^D \log(\hat p_j) \end{equation}$$ and we show that the sampling variance is
$$\begin{equation} \tag{2} \text{var}[\text{clr}_i({\bf \hat p})] = \frac{\tau}{C} \left[ \frac{1}{\hat p_i} - \frac{2}{ D \hat p_i} + \frac{1}{D^2}\sum_{j=1}^D \frac{1}{\hat p_j} \right]. \label{eqn2} \end{equation}$$
Simulations
The sampling variance is derived from asymototic theory, so we examine its behavior for finite total counts. Here we evaluate the empirical variance from draws from a Dirichlet-multinomial distribution while varying , , . A pseudocount of 0.5 is added to the observed counts since the asymptotic theory is not defined for counts of zero.
Here we plot the standard deviation after CLR transform from the empirical DMN and the asymptotic normal approximation under a range of conditions. Results are shown for instances with at least 2 counts.
Interpretation
The asymptotic standard deviation shows good agreement with the empirical results even for small values of , when at least 2 counts are observed. In practice, it is often reasonable to assume a sufficient number of counts before a variable is included in an analysis. Importantly, with less than 2 counts the asymptotic theory gives a larger standard deviation than the emprical results (results not shown). Therefore, this approach is conservative and should not underestimate the true amount of variation. The asymptotic normal approximation is most accurate for large total counts , large proportions , and small overdispersion .
Consideration of overdispersion
Based on Equation (2), the variance of the CLR-transformed proportions is a linear function of . Importantly, downstream analysis of the CLR-transformed proportions with a precision-weighted linear (mixed) model or a variance stabilizing transform depends only on the relative variances. Since relative variances are invariant to the scale of , for these applications the value of can be set to 1 instead of being estimated from the data.
For other applications, crumblr can estimate
from the data by using crumblr(counts, tau=NULL). This
calls dmn.mle() to estimate the parameters of the DMN
distribution and is substantially faster than alternatives.
Session Info
## R version 4.4.1 (2024-06-14)
## Platform: aarch64-apple-darwin23.5.0
## Running under: macOS Sonoma 14.7.1
##
## Matrix products: default
## BLAS: /Users/gabrielhoffman/prog/R-4.4.1/lib/libRblas.dylib
## LAPACK: /opt/homebrew/Cellar/r/4.4.2_2/lib/R/lib/libRlapack.dylib; LAPACK version 3.12.0
##
## locale:
## [1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
##
## time zone: America/New_York
## tzcode source: internal
##
## attached base packages:
## [1] parallel stats graphics grDevices utils datasets methods base
##
## other attached packages:
## [1] lubridate_1.9.4 forcats_1.0.0 stringr_1.5.1 dplyr_1.1.4 purrr_1.0.4
## [6] readr_2.1.5 tidyr_1.3.1 tibble_3.2.1 tidyverse_2.0.0 glue_1.8.0
## [11] HMP_2.0.1 dirmult_0.1.3-5 crumblr_0.99.19 ggplot2_3.5.1 BiocStyle_2.34.0
##
## loaded via a namespace (and not attached):
## [1] jsonlite_1.8.9 magrittr_2.0.3 farver_2.1.2
## [4] nloptr_2.1.1 rmarkdown_2.29 fs_1.6.5
## [7] zlibbioc_1.52.0 ragg_1.3.3 vctrs_0.6.5
## [10] minqa_1.2.8 ggtree_3.14.0 htmltools_0.5.8.1
## [13] S4Arrays_1.6.0 broom_1.0.7 SparseArray_1.6.1
## [16] gridGraphics_0.5-1 variancePartition_1.36.3 sass_0.4.9
## [19] KernSmooth_2.23-26 bslib_0.9.0 htmlwidgets_1.6.4
## [22] desc_1.4.3 pbkrtest_0.5.3 plyr_1.8.9
## [25] cachem_1.1.0 lifecycle_1.0.4 iterators_1.0.14
## [28] pkgconfig_2.0.3 Matrix_1.7-2 R6_2.6.1
## [31] fastmap_1.2.0 GenomeInfoDbData_1.2.13 rbibutils_2.3
## [34] MatrixGenerics_1.18.1 digest_0.6.37 numDeriv_2016.8-1.1
## [37] aplot_0.2.4 colorspace_2.1-1 patchwork_1.3.0
## [40] S4Vectors_0.44.0 textshaping_1.0.0 GenomicRanges_1.58.0
## [43] vegan_2.6-10 labeling_0.4.3 RcppZiggurat_0.1.6
## [46] timechange_0.3.0 mgcv_1.9-1 httr_1.4.7
## [49] abind_1.4-8 compiler_4.4.1 aod_1.3.3
## [52] withr_3.0.2 backports_1.5.0 BiocParallel_1.40.0
## [55] viridis_0.6.5 gplots_3.2.0 MASS_7.3-64
## [58] DelayedArray_0.32.0 corpcor_1.6.10 permute_0.9-7
## [61] gtools_3.9.5 caTools_1.18.3 tools_4.4.1
## [64] ape_5.8-1 remaCor_0.0.18 nlme_3.1-167
## [67] grid_4.4.1 cluster_2.1.8 reshape2_1.4.4
## [70] generics_0.1.3 gtable_0.3.6 tzdb_0.4.0
## [73] hms_1.1.3 XVector_0.46.0 BiocGenerics_0.52.0
## [76] foreach_1.5.2 pillar_1.10.1 yulab.utils_0.2.0
## [79] limma_3.62.2 splines_4.4.1 treeio_1.30.0
## [82] lattice_0.22-6 tidyselect_1.2.1 SingleCellExperiment_1.28.1
## [85] knitr_1.49 reformulas_0.4.0 gridExtra_2.3
## [88] bookdown_0.42 IRanges_2.40.1 SummarizedExperiment_1.36.0
## [91] RhpcBLASctl_0.23-42 stats4_4.4.1 xfun_0.50
## [94] Biobase_2.66.0 statmod_1.5.0 matrixStats_1.5.0
## [97] stringi_1.8.4 UCSC.utils_1.2.0 lazyeval_0.2.2
## [100] ggfun_0.1.8 yaml_2.3.10 boot_1.3-31
## [103] evaluate_1.0.3 codetools_0.2-20 rpart.plot_3.1.2
## [106] BiocManager_1.30.25 ggplotify_0.1.2 cli_3.6.4
## [109] rpart_4.1.24 RcppParallel_5.1.10 systemfonts_1.2.1
## [112] Rdpack_2.6.2 munsell_0.5.1 jquerylib_0.1.4
## [115] Rcpp_1.0.14 GenomeInfoDb_1.42.3 EnvStats_3.0.0
## [118] Rfast_2.1.4 pkgdown_2.1.1 bitops_1.0-9
## [121] lme4_1.1-36 viridisLite_0.4.2 mvtnorm_1.3-3
## [124] tidytree_0.4.6 lmerTest_3.1-3 scales_1.3.0
## [127] crayon_1.5.3 fANCOVA_0.6-1 rlang_1.1.5